Real Nos.
Different Types of Real Nos.
- A number that can be represented as a point on the number line is a Real No.
- Such number line is called Real No. Line.
- There are several types of numbers within the Real No. Line.
- In Elementary/ Primary schools, understanding of Natural nos. and some knowledge on fractions is good enough for Math study.
- In middle/ high schools, Directed nos., Rational and Irrational nos. are introduced.
Definitions
- Natural nos. : \( \{1, 2, 3, \ldots \} \ \) denoted by the set \( \mathbb{N} \ \) [some authors include integer 0]
- Integers : \( \{\ldots , -2, -1, 0, 1, 2, \ldots \} \) denoted by the set \(\mathbb{Z}\)
- Rational nos. : $\big\{ \frac{p}{q}\big |\; p, q \in \mathbb{Z},\; q \neq 0 \big\} \ $ denoted by the set $\mathbb{Q}$
- Irrational nos. : $ \mathbb{R} {\setminus} \mathbb{Q}$
- Surds $\subseteq \mathbb{R} {\setminus} \mathbb{Q}$. Examples are: square root $ (\sqrt{\phantom{x}}) $, cube root $ (\sqrt[3]{\phantom{x}}) $ form, and so on.
Misconceptions
- Fractions and Rational nos. seems to be the same but they are different. All fractions are Rational nos., not all rational nos. are fractions. By definition, all integers are Rational nos., but integers are commonly considered different from fractions.
- All decimal nos. can be expressed in the form of Rational nos. no matter recurring or finite decimal. Thus, the set of decimal nos. is not a separate type of Real nos., it is a subset of Rational nos.
Problem Solving Techniques
I. Convert a recurring decimal no. to fraction, e.g. \( 0.23\dot 45\dot 6 \)
- Decompose non-recurring and recurring part of the decimal
- Construct a fraction with denominator having 9 for each recurring digit and 0 for each non-recurring digit. 有循環就9, 無循環就0, 先9後0, and with recurring digits as numerator.
For this example,
$$ \begin{aligned}0.23\dot 45\dot 6 &= 0.23 + 0.00\dot 45 \dot 6 \\[.5em] &= \frac{23}{100} + \frac{456}{99900} \\[.5em] &= \frac{23(999)+456}{99900} \\[.5em] &= \frac{23433}{99900} \\[.5em] &= \frac{7811}{33300} \end{aligned} $$Textbook method,
$$ \begin{aligned} \text{Let}\quad x &= 0.23\dot 45 \dot 6, \\[.5em] 100000x &= 23456.456456 \cdots &(1)\\ 100x &= 23.456456 \cdots &(2) \\[.5em] (1)-(2), & \text{ we have} \\[.5em] 99900x &= 23433 \nonumber \\[.5em] x &= \frac{23433}{99900} \\[.5em] &= \frac{7811}{33300} \end{aligned} $$II. Rationalize Denominator, e.g. \(\dfrac{c}{\sqrt{a}+\sqrt{b}} \)
Using identity: $ \ \color{tomato}{\boxed { \color{RoyalBlue} {(x+y)(x-y)\equiv x^2-y^2}}} $
Complex Nos.
To solve equations like the following, we need to expand number system from Real nos.:
$$ \begin{equation} z^2+1=0 \end{equation} $$
Since there is no Real number, say $ x \in\mathbb{R} $ such that $$ x^2 = -1 $$
$ i=\sqrt{-1} $, the Imaginary unit of Complex No. is introduced.
Definitions
- $ i = \sqrt{-1}, \mbox{ i.e. } i^2 = -1 $
- For all $C = a + bi \ $ where $ a, b $ are Real nos., we call $C$ a Complex No., and denote the set of Complex No. as $ \mathbb{C} $.
- For all $C = a+ bi, $
- $a$ is the Real part
- $b$ is the Imaginary part
- $bi$ is the Imaginary unit
- in particular if $b = 0, $ then $C$ is also a Real no., otherwise $b\neq 0 , $ it is either a non-Real Complex no. or purely Imaginary no.
Misconceptions
- Both the Real part, $ a $ and Imaginary part, \(b\) are Real nos.
- Don’t confuse the Imaginary part, $b$ with the Imaginary unit \(bi\)!
- Don’t assume any Complex No. be non-Real! Acutally, $\, \mathbb{R} \subseteq \mathbb{C} $. That is, all Real nos. belong to the set of Complex Nos. — extension of Real no. set.
Problem Solving Techniques
I. Simplify $ \dfrac{a+bi}{c+di} $ where $ d \neq 0 $
Using identity: $ \ \color{Tomato}{ \boxed{ \color{RoyalBlue}{(c+di)(c-di) \equiv c^2 – (di)^2 }} } $
the Imaginary unit in the denominator of the rational expression can be eliminated, i.e.
$ \begin{align}
\frac{a+bi}{c+di} &= \frac{a+bi}{c+di} {\cdot} \dfrac{c-di}{c-di}\\[.5em]
&=\frac{(a+bi)(c-di)}{c^2-(di)^2}\\[.5em]
&=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2} \\[.5em]
&= \frac{ac+bd}{c^2+d^2}+ \frac{bc-ad}{c^2+d^2}i \end{align} $
II. Compute \(i^k \), for some large integer \(k\), say \(i^{2689}\)
Using the facts:
- $ i^4 = 1$ $ \; \left[ \because i^2 \times i^2 = (-1)(-1) \right] $
- If the number composed of the last 2 digits of an integer is divisible by 4, then that integer must be divisible by 4.
In case of 2689, though it is indivisible by 4, try the largest integer < 2689 and check if it’s divisible by 4,
$ \quad \color{Tomato} { \boxed{ \color{RoyalBlue}{\; \begin{aligned} 26 &\underline{88} \\ &\uparrow \\ &\text{Check the last 2 digits} \\ &\text{88 is divisible by 4} \end{aligned} }} }\\[3em] \quad \begin{align*} \therefore \; i^{2689} &= i^{2688+1} \\ &= i^{2688} \times i \\ &= 1 \times i = i \end{align*} \\[1em] $Together with the facts
$ \quad \color{Tomato}{ \boxed{ \; \color{RoyalBlue}{\begin{align*}i^2 &= -1\\ i^3 &= -i \\ i^{-1} &= -i \end{align*} }} }\\\; i^k \textrm{ can be computed } \forall k \in \mathbb{Z}. \\[1em]$
III. Comparing Real and Imaginary parts:
$ \quad \color{Tomato}{ \boxed{ \color{RoyalBlue}{ \begin{align*} & a+bi = c+di \\ \Leftrightarrow \ & a=c \, , \; b=d \end{align*} }} \\[1em] }$A special scenario: if $a+bi = 0 $
then $ a+bi=0+0i, \mbox{ i.e. } a=b=0 $
Concepts of Function
Why need Functions?
Finding out the relationship between variables is useful in all kinds of knowledge. In real world, it is common that one quantity depends on the another quantity.
For example, the overtime salary of a worker depends on the quantity of extra working hours and the hourly rate of overtime.
Definitions
A relation between the elements of two sets \(A\) and \(B\) is a function, \(f\) from \(A\) to \(B\) if:
- for each element $x \in A, $ there is an assigned element $y \in B $ usually written as $ y = f(x) ; $
- for any $ x_1, x_2 \in A $ assigned to $ y_1, y_2 \in B $ respectively, if $x_1 = x_2 $ then $y_1 = y_2. $
- set \(A\) is called the Domain of $f$
- set \(B\) is called the Codomain of $f$
- Range (Image) of $ \, f: $ $ \quad f(A) = \{f(x) \in B \; | \; x \in A\} $
- $ f \ $ is also called a mapping from $ A \mbox{ to } B, \ $ denoted by $ \ f:A \to B $
A function can be represented in several forms, including:
I. Functions in Algebraic Form (also known as Algebraic Functions)
Algebraic expression usually can represent a function, e.g.
$ \quad f(x)=3x^2-x-4 \\[.2em] $In this example,
- Domain: \(\mathbb{R}\)
- Range: \(\{y \in \mathbb{R}\; | \; y \geq -\frac{49}{12}\}\)
[why? To be discussed in online class]
II. Functions in Graphical Form
Functions are commonly represented by graphs, especially continuous function.
The graph of a function \(f\) is the collection of all ordered pairs \((x, f(x)) \\[.2em]\).
Example – Quadratic Functions
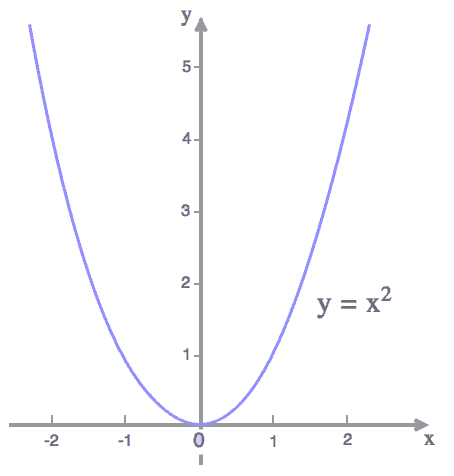
In this example,
- Domain: \( \mathbb{R}\)
- Range: \(\{y \in \mathbb{R}\; | \; y \geq 0 \}\)
III. Functions in Table-Form
Tables can also be used to describe functions, e.g.
| Input | -1 | -2 | -3 | -7 | -8 | |
| Output | 1 | 3 | 2 | 4 | 1 |
In this example,
- Domain: \( \{-1, -2, -3, -7, -8\}\)
- Range: \(\{1, 2, 3, 4\}\)
IV. Functions in Venn Diagram
Because sets can usually be represented by Venn diagrams, sometimes a function is represented by Venn diagrams with arrows connecting the elements from the Domain to Codomain of the function.
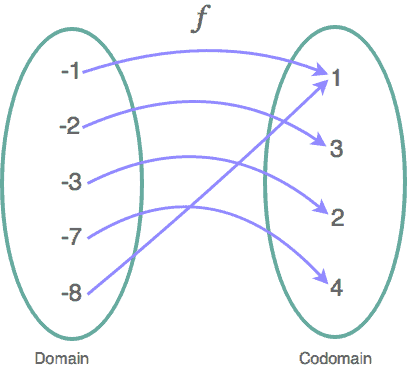
Misconceptions
- Though a function is a graph, by definition, not all graphs are functions, e.g. $ \ y^2=x \enspace $
[why? To be discussed in online class] - Only test condition ii. above in definitions whether a relation is a function, but missed to testing condition i. (for each element in \(A\) there is assigned element in \(B\))
- The notation \(f(x)\) appears in Algebraic functions, but not necessary for all types functions, e.g. in Table-form.
Exponents & Log
Why need Exponents
When a number, say \(a\) multiplies itself several times, the expression can be written as either the LHS or RHS of the equation below:\[ \underbrace{a \times a \times \ldots \times a}_{\color{RoyalBlue}{k\text{ times}}} = a^k \]
- Using exponent in the RHS of the above identity makes LHS simpler.
- The exponent \(k\) can be extended from a positive integer to any Rational no. and even beyond [to be covered by college-level Math]
- If \(k\) is positive non-integer, then \[k = p/q \quad \text{where } p,q \in \mathbb{Z}\] and \(a^k\) means \(a\) multiplies itself \(p\) times and takes \(q^{\rm th}\) root, i.e. $$ \begin{align} a^\frac{p}{q} &= (a^p)^\frac{1}{q} \\ &= \raise{.8ex} \sqrt[q \uproot1]{ } \underbrace{ \overline{a \times a \times \cdots \times a}}_{ \color{RoyalBlue}{p\ \text{times}}} \end{align} $$
- In measuring extremely tiny or extremely big quantities, e.g. the term “nanometer” means \(10^{-9}\) meter; speed of light is approximately \(3 \times 10^8\) m/s.
Definitions
Exponents
- In an expression \(a^k\), \(a\) is called the base and \(k\) is called the exponent or index.
- A function involving exponent is called exponential function.
- \(a^0 = 1,\) for all \( a \neq 0 \)
- \(0^k = 0,\) for all \( k \neq 0 \)
- \(0^0\) is undefined
Logarithms
- $ \log_a x = y \text{ means } a^y = x , $ $ a$ is a non-zero Real no.
- \(a\) is called the base and \(y\) is called the exponent.
- In log expressions, when the base \(a\) is equal to 10, i.e. \( \log_{10}x \), it is usually denoted by \(\log x\) (no need to write 10 as the base).
- When studying Further Math, need to know that when the base \(a\) is equal to constant e, i.e. \(\log_e x\), we call it the natural log of \(x\), written as \(\ln x\).
Properties
For the properties below, \(\, a, b, m, n \in \mathbb{R} {\setminus} \{0\} \\[1em]\)
Exponents
- \(a^m \cdot a^n = a^{m+n}\)
- \( (a^m)^n = a^{m \cdot n} \)
Logorithms
- $ \log_a mn = \log_a m + \log_a n $
- $ \log_a \dfrac{m}{n} = \log_a m-\log_a n $
- $ \log_a m^n = n\log_am $
- $ \log_a m = \dfrac{\log_b m}{\log_b a} $
Problem Solving Techniques
I. Find the unknown of exponential equation: \(\, a^x = b\).
Take Log to base 10 of both sides,
\[\begin{aligned}\log a^x &= \log b \\ x \log a &= \log b \quad \small\text{[use Prop. 3]}\\ x &= \dfrac{\log b}{\log a} \end{aligned}\]
Example
The figure below shows the graph of $ f(x) = q^{-x} $ and the graph of $ g(x) = r^{-x} $ on the same rectangular coordinate plane, where $q$ and $r$ are positive constants. If a vertical line $l$ cuts the $x$-axis, the graph of $y=f(x)$ and the graph of $y=g(x)$ at $P, \, $ $Q \ $ and $R$ respectively, show that
$\begin{array}{ll}
\mbox{a)} & q > r \\[.5em]
\mbox{b)} & q + r > 2 \\[.5em]
\raise{1.5ex} \mbox{c)} & \dfrac{\log PQ}{\log PR} = \log_r q \\
\end{array} $
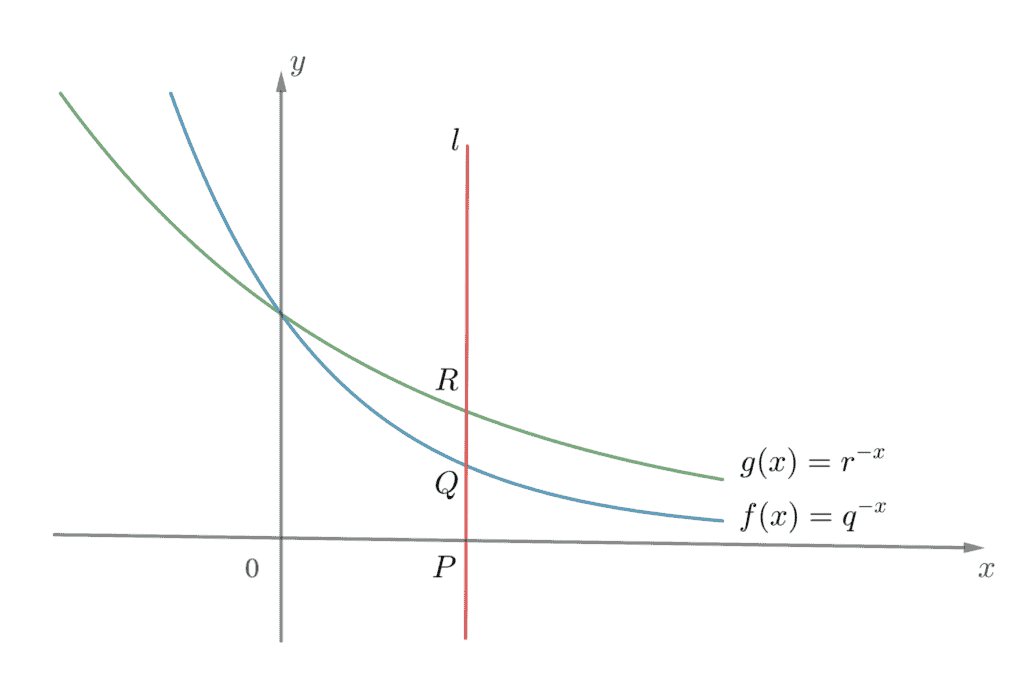
Solution:
$ \mbox{a)} \quad \mbox{from the graph } g(x) > f(x) \ \mbox{for all } x>0, \\
\kern3.5ex \mbox{put } x=1, \\
\kern3.5ex \begin{align}
g(1) &> f(1) \\
r^{-1} &> q^{-1} \\
q &> r \\
\end{align} $
$ \mbox{b)} \quad \mbox{shape of }\, y=f(x) \mbox{ is determined by } r, \\[.5em]
\phantom{b)} \quad \begin{array}{rl}
\mbox{(i)} & \mbox{if } r<1, \mbox{ increasing function}\\
\mbox{(ii)} & \mbox{if } r=0, \mbox{ a straight line}\\ \mbox{(iii)} & \mbox{if } r>1, \mbox{ decreasing function}\\
\end{array} \\[2em]
\quad \mbox{similar to } y=g(x) , \mbox{and } \\
\quad \mbox{obviously both } f, g \mbox{ are decreasing} \\
\quad \mbox{we have } r>1, q>1, \mbox{ thus } r+1>2 \\
$
$ \mbox{c)} \quad \mbox{Let } P = (a,0), \ a>0 \\[.6em]
\quad \begin{align}
\dfrac{\log PQ}{\log PR} &= \dfrac{\log q^{-a}}{\log r^{-a}} \\[.2em]
&= \dfrac{-a \log q}{-a \log r} \\[.2em]
&= \dfrac{\log q}{\log r} \\[.2em]
&= \log_r q \\
\end{align}
$
Inequalities
Why are Inequalities Important?
Sometimes we do not know exactly the value of an unknown, but we know the boundaries of possible values.
Long before having the knowledge of Irrational nos., people knew that the circumference to diameter ratio, \(\pi\) is greater than 3. And 3 is then the lower bound of \(\pi\). People then worked hard to narrow down the boundaries (both lower and upper bounds) of \(\pi\) and getting more and more accurate value of it although its exact value can neither be written as a fraction nor a decimal figure because it is an irrational no.
Certain inequalities are particularly important in algebra. Besides Linear Programming, concepts of inequalities are frequently used in other areas, like Graph of Functions, Geometric Sequences and Arithmetic Sequences, etc.
Elementary Properties
$ \mbox{Given} \; \color{Tomato}{\boxed{ \color{RoyalBlue}{a > b}} } \color{DimGray}{\, \text{, where } a,\, b \in \mathbb{R} } \\[0.5em] \enspace \begin{aligned} &a+x > b+x \quad \forall x \in \mathbb{R} \quad &\color{RoyalBlue}{(1.1)} \\[0.5em] \, &ax > bx \; \text{ when } x >0, \text{ but} \\ &ax < bx \;\text{ when } x <0 \quad &\color{RoyalBlue}{(1.2)} \\[0.5em] \, &\dfrac{1}{a}< \dfrac{1}{b} \; \text{when } ab>0, \text{ but}\\[0.2em] &\dfrac{1}{a} > \dfrac{1}{b} \; \text{when }ab<0 \quad &\color{RoyalBlue}{(1.3)} \end{aligned} \\[2em] $Please note that in (1.3), \(ab >0\) means they are of the same sign.
Example
Quadratic Inequalities
Considering a quadratic equation, if the equal sign is replaced by an inequality sign, then it becomes a Quadratic Inequality.
Steps of Solving Quadratic Inequalities:
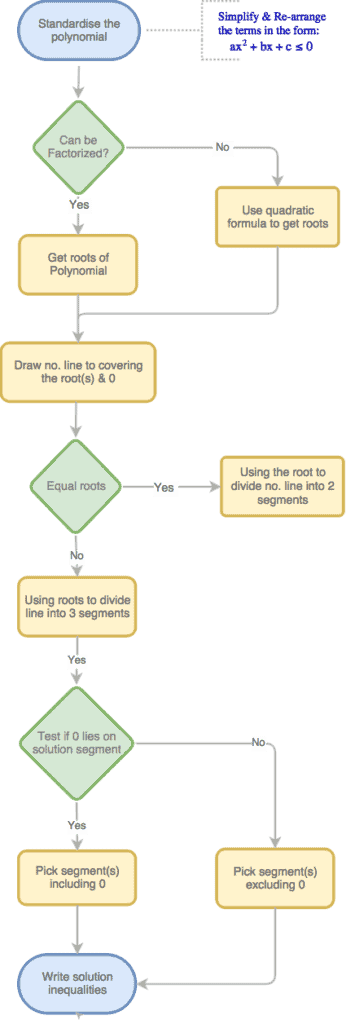
Recall the Quadratic Formula:
$$ \color{Tomato}{ \boxed{ \tiny \phantom{xxx} \\ \; \color{RoyalBlue}{x = \dfrac{-b \pm \sqrt {b^2-4ac}}{2a} \; \\[.3em] }}} $$Polynomial
Definitions
- Either a number or a number (called coefficient) multiplied by a variable is called a/an (algebraic) term
- 2 terms with the same variables raised to the same power, no matter if the numbers are the same are called like terms
- Algebraic expression is an expression made up of adding multiple algebraic terms.
- Polynomial is a kind of algebraic expression with a restriction that the power/exponent/index of the variable(s) must be non-negative integers
- Polynomial with one, two and three terms are called monomials, binomials, and trinomials respectively.
- The degree of a polynomial is the maximum value of the sums of the exponents of the variables in each term
- If a polynomial can be expressed as a product of polynomials, then the process of factoring this polynomial to the maximum no. of factors is called factorization
Useful Identities for Factorization
Identities are special kind of equations such that the left-hand-side (L.H.S.) is equal to the right-hand-side (R.H.S.) for all possible values of the variables, and the equation sign may be denoted by the equivalent sign $ \equiv . $
- $ x^2 – y^2 \equiv (x+y)(x-y) $
- $ x^2 + 2xy + y^2 \equiv (x+y)^2 $
- $ x^2-2xy + y^2 \equiv (x-y)^2 $
- $ x^3 + y^3 \equiv (x+y)(x^2-xy + y^2) $
- $ x^3-y^3 \equiv (x-y)(x^2+xy+y^2) $
Example
Factorize:
$ \mbox{ a) } \quad a^2- b^2-2a +1 \\ \mbox{ b) } \quad 3x^3- 24 \\[.5em] $Solution:
$ \begin{align} \mbox{ a) } \quad & a^2-b^2-2a+1 \\ = \, & (a^2-2a+1)-b^2 \\ = \, & (a-1)^2-b^2 \\ = \, &(a-1+b)(a-1-b) \\[.5em] \mbox{ b) } \quad & 3x^3-24 \\ = \, & 3(x^3-8) \\ = \, & 3(x^3-2^3) \\ = \, & 3(x-2)(x^2+2x+4) \\ \end{align} $Remainder & Factor Theorems
The Remainder Thm. states that
if a polynomial $ f(x) $ is divided by $ x-a $, then the remainder
$ \quad R = f(a). $
Consider the divisor $(x-a)$ of the polynomial $f(x)$ with quotient $Q(x)$ and the remainder $R, \ $ we have:
$ \quad \begin{align} f(x) &= (x-a)Q(x) + R, \\[.3em] \mbox{ put } x &= a, \mbox{ we have } \\[.3em] f(a) &= (a-a)Q(a) + R \\ &= R \end{align} \\[2em] $Example
When $ {kx}^2 + x -1 \, $ is divided by $ x+2, \, $ the remainder is 1. Find $k.$
Solution:
$ \mbox{Let } \, f(x) = kx^2+x-1 \\ \begin{align} \because \kern4.5em f(-2) &= 1 \\ \therefore k(-2)^2+(-2)-1 &= 1 \\ 4k-3 &= 1 \\ k &= 1 \end{align} $The Factor Thm. states that
a polynomial $ f(x) $ has a factor $ \, (x-k) \, $ if and only if $ \, f(k) = 0 $
Example
Let $ \, f(x) = 4x^3-8x^2-3x+9 $
$ \begin{align} \mbox{a) } & \mbox{ Show that } \, x+1 \, \mbox{ is a factor of } \, f(x) \\[.5em] \mbox{b) } & \mbox{ Factorize } f(x) \\[.5em] \mbox{c) } & \mbox{ Given that } g(x) = x(x+1)^2(2x-3)^3 \\ & \mbox{ Find the H.C.F. and L.C.M. of } \\ & \quad f(x) \mbox{ and } g(x). \\ \end{align} $Solution:
$ \begin{align} \mbox{a)} \quad f(-1) &= 4(-1)^3-8(-1)^2-3(-1) + 9 \\ &= {-4}-8+3+9 \\ &=0 \end{align} \\ \qquad \therefore x+1 \mbox{ is a factor of } f(x) \\[1.5em] $$ \require{enclose} \begin{array}{lr} \mbox{b) } & \kern-4ex 4x^2-12x+9 \\[-3pt] & x+1 \enclose{longdiv}{4x^3- \phantom{0}8x^2- \phantom{0}3x+9} \\[-2ex] & \underline{4x^3+ \phantom{0} 4x^2} \kern9ex \\ & -12x^2- \phantom{0} 3x \kern3.5ex \\[-2ex] & \underline{ -12x^2-12x} \kern3.5ex \\[-3pt] & 9x+9 \\[-2ex] & \underline{9x+9} \\[.6em] & \therefore f(x) = (x+1)(4x^2-12x+9) \\ & = (x+1)(2x-3)^2 \kern5.5ex \\ \end{array} $
$ \begin{array}{lll} \mbox{c) } & \mbox{H.C.F.} &\kern-2ex = (x+1)(2x-3)^2 \\ & \mbox{L.C.M.} &\kern-2ex = x(x+1)^2(2x-3)^3 \\ \end{array} $